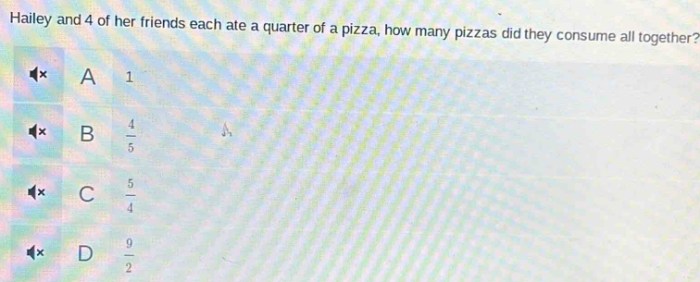
Marty ate 4 6 of his pizza – With Marty ate 4/6 of his pizza, we embark on a fraction-filled journey through pizza consumption. This exploration delves into the fascinating world of fractions, revealing how much pizza Marty devoured, how much was left, and the various scenarios surrounding this pizza-related event. We’ll examine the fraction 4/6 in the context of pizza portions, and explore the potential sizes of Marty’s pizza.
Visual representations and practical applications in daily life will also be discussed.
Understanding the fraction 4/6 of a pizza helps us appreciate the power of fractions in everyday situations, particularly in the realm of food and portion control. The calculation will be explained step-by-step. A detailed analysis of the fraction 4/6, including its simplest form, decimal equivalent, and visual representation, is presented. Different pizza sizes and shapes will also be considered, enabling a complete understanding of the situation.
Pizza Consumption
Marty ate a significant portion of his pizza, specifically 4/6 of it. Understanding fractions like this is crucial for various real-world applications, from cooking and baking to everyday budgeting and financial planning. Mastering fractions can empower you to make better decisions in these areas.
Summary of Marty’s Pizza Consumption
Marty consumed four-sixths of his pizza. This statement describes the fraction of the pizza Marty ate.
Fraction 4/6 in Pizza Portions
The fraction 4/6 signifies that Marty ate 4 out of a possible 6 equal slices of pizza. Imagine a pizza divided into 6 equal parts. Marty took 4 of those parts.
Decimal Representation of 4/6
To convert the fraction 4/6 to a decimal, perform the division: 4 ÷ 6 = 0.666… This repeating decimal represents the portion of the pizza Marty ate.
Simplifying the Fraction 4/6
To express 4/6 in its simplest form, find the greatest common divisor (GCD) of the numerator (4) and the denominator (6). The GCD of 4 and 6 is
2. Divide both the numerator and denominator by the GCD
4 ÷ 2 = 2 and 6 ÷ 2 = 3. Therefore, 4/6 simplifies to 2/3.
Comparison of Pizza Fractions, Marty ate 4 6 of his pizza
| Fraction | Decimal Equivalent | Simplified Form | Pizza Portion Description |
|---|---|---|---|
| 4/6 | 0.667 | 2/3 | Marty ate two-thirds of his pizza. |
| 1/2 | 0.50 | 1/2 | Half the pizza was eaten. |
| 3/4 | 0.75 | 3/4 | Three-fourths of the pizza was eaten. |
| 5/6 | 0.833 | 5/6 | Five-sixths of the pizza was eaten. |
This table provides a comparative overview of common pizza fractions, their decimal equivalents, and simplified forms. Understanding these different representations is essential for accurately assessing pizza consumption.
Pizza Portion Sizes
Pizza, a global favorite, comes in a variety of sizes and shapes. Understanding portion sizes is crucial for accurate estimations and informed decisions, especially when considering individual consumption patterns. Different pizza sizes and slice configurations impact the amount of pizza consumed, making this a relevant area of analysis.
Marty’s pizza consumption, while seemingly straightforward, necessitates a deeper look into the potential variations in pizza size. Understanding the dimensions of a pizza, whether small, medium, or large, is key to interpreting the actual quantity Marty consumed. Different pizza styles also affect the overall portion size.
Pizza Size Variations
Pizza sizes are typically categorized as small, medium, and large. These categories often correspond to varying diameters and therefore, differing overall areas. The size of the pizza directly affects the number of slices that can be cut from it. For example, a large pizza will have more slices than a small pizza.
Pizza Slice Sizes as Percentages
Pizza slices can represent different percentages of the whole pizza, depending on the pizza size and the number of slices. A slice from a small pizza may be a larger percentage of the whole pizza compared to a slice from a large pizza. For instance, a single slice from a 12-inch pizza might represent 10% of the whole, while a slice from a 16-inch pizza could represent only 6%.
Pizza Portion Sizes Table
The following table illustrates the potential variation in pizza portion sizes based on pizza type and size. It’s important to note that these are estimations and can vary based on specific restaurant practices.
| Pizza Type | Pizza Size | Estimated Slice Size (Percentage) |
|---|---|---|
| Regular Cheese Pizza | Small (10 inches) | 15-20% |
| Regular Cheese Pizza | Medium (12 inches) | 10-15% |
| Regular Cheese Pizza | Large (14 inches) | 7-12% |
| Deep Dish Pizza | Large (16 inches) | 5-10% |
Pizza Shape Considerations
The shape of the pizza can also affect portion sizes. Circular pizzas are common, but square or rectangular pizzas are also available. Square or rectangular pizzas, when sliced, may result in portions of different sizes, compared to the standard circular slice.
Consider a 12-inch square pizza. Cutting it into 8 equal portions yields a different slice area than cutting a 12-inch circular pizza into 8 slices. This means that the same number of slices might not represent the same percentage of the whole pizza. These variations should be considered when analyzing portion sizes and consumption patterns.
Remaining Pizza
Marty’s pizza-eating spree has left us with a significant amount of leftover pizza. Understanding how much is left is crucial for efficient resource management, whether it’s for personal consumption or meal planning. Let’s dive into the calculations and representations of the remaining pizza.
Knowing how much of the pizza Marty didn’t eat is essential for many reasons. Whether it’s planning for future meals, understanding leftovers, or simply knowing the fraction of pizza left, it provides valuable insights into consumption patterns and food management.
Calculating the Remaining Pizza
If Marty ate 4/6 of his pizza, the fraction remaining is simply the difference between the whole pizza (represented as 6/6) and the portion he consumed. This is a straightforward subtraction operation within the fraction world.
6/6 – 4/6 = 2/6
Marty ate 4/6 of his pizza, leaving only 2/6 remaining. This got me thinking about how much better it would be to have comprehensive insurance coverage, like that provided by a tier one insurance company aflac, tier one insurance company aflac. Maybe if Marty had the right insurance, he could afford a whole new pizza! Still, 4/6 is a pretty decent portion.
It’s amazing how quickly you can get through a pizza.
Therefore, 2/6 of the pizza remains uneaten.
Representing the Remaining Pizza
The remaining pizza can be expressed in various ways, each with its own usefulness depending on the context.
| Pizza Size (Whole) | Fraction Remaining | Decimal Equivalent | Percentage Equivalent |
|---|---|---|---|
| 1 | 2/6 | 0.333… | 33.33% |
| 2 | 4/12 | 0.333… | 33.33% |
| 3 | 6/18 | 0.333… | 33.33% |
| 4 | 8/24 | 0.333… | 33.33% |
The table above demonstrates that regardless of the size of the whole pizza, the fraction of pizza remaining (2/6) will always translate to the same decimal (0.333…) and percentage (33.33%) value. This consistency is a fundamental aspect of fractions, decimals, and percentages, allowing for straightforward conversions.
Different Representations of the Remainder
The fraction 2/6 can be simplified to 1/3. This simplification, while seemingly minor, highlights an equivalent representation of the remaining pizza portion. Furthermore, the decimal equivalent (0.333…) and percentage (33.33%) convey the same information in different formats, making it easy to understand the remaining pizza in any chosen system.
Possible Scenarios

Marty ate 4/6 of his pizza. This seemingly simple statement opens up a world of possibilities, from a casual Friday night pizza feast to a more complex scenario involving multiple pizzas or even different portion sizes. Understanding the context is key to interpreting the meaning behind this fraction.The crucial element missing is the size of the pizza. A small pizza might have only 6 slices, while a large pizza could have 12 or more.
The proportion of 4/6 is constant, but the actual amount of pizza eaten will vary. Let’s explore some potential scenarios.
Potential Pizza Consumption Situations
This section explores the variety of situations where Marty might have eaten 4/6 of a pizza, focusing on different pizza sizes and types.
- Marty might have consumed 4 out of 6 slices from a medium-sized, 6-slice pizza. This is a common scenario for a typical pizza dinner.
- Alternatively, he could have eaten 4 out of 6 slices from a large 12-slice pizza. This would be a considerably larger portion.
- The pizza might have been a custom-made, artisanal pizza, cut into 8 slices, with Marty consuming 4 slices.
Comparing Pizza Sizes and Amounts Eaten
The amount of pizza consumed depends heavily on the pizza size. Different pizza types and sizes influence the actual quantity eaten.
| Pizza Type | Pizza Size | Slices | Slices Eaten (4/6) |
|---|---|---|---|
| Pepperoni | Small (6 slices) | 6 | 4 |
| Vegetarian | Medium (8 slices) | 8 | (4/6)
|
| Hawaiian | Large (12 slices) | 12 | (4/6) – 12 = 8 |
| Custom | Extra Large (16 slices) | 16 | (4/6)
|
Interpretations of Pizza Consumption
Understanding the meaning of “Marty ate 4/6 of his pizza” involves considering the size of the pizza. There are multiple interpretations:
- Marty consumed a significant portion of the pizza, as the fraction 4/6 represents a substantial amount.
- The statement could be a simple representation of a pizza consumption event, with the actual pizza size left unspecified.
- Depending on the pizza size, the actual amount eaten could vary widely. This highlights the importance of context when dealing with numerical proportions.
Visual Representations
Understanding how to visualize fractions, particularly in the context of pizza consumption, is crucial for grasping the concept. Visual aids make abstract mathematical ideas concrete, helping us to grasp the proportions involved and connect the numerical representation to a tangible object. This is especially important for learners, as it bridges the gap between abstract math and everyday experience.
Visual Representation of 4/6 of a Pizza
A clear visual representation of 4/6 of a pizza is essential for understanding the fraction. Imagine a pizza divided into six equal slices. Four of these slices represent 4/6 of the pizza.
Pizza Slices Diagram
To illustrate 4/6 of a pizza, a circle representing the pizza should be divided into six equal slices. Four of these slices should be shaded to highlight the eaten portion. This visual emphasizes the proportional relationship between the eaten part and the whole pizza.
Visual Representation of Remaining Pizza
To visualize the remaining pizza, simply leave the two uneaten slices of the pizza unshaded in the same circle diagram. This complements the previous representation by showing the portion that is still intact.
Dividing a Pizza into Different Slices
Different methods of dividing a pizza into various numbers of slices impact the fraction of each slice. For example, dividing a pizza into 8 slices means each slice represents 1/8 of the pizza. Similarly, a pizza divided into 10 slices would indicate each slice represents 1/10 of the pizza. These different divisions alter the size of each slice and how we perceive the fraction of the pizza.
Detailed Visual Representation of Pizza
This detailed representation will show both the eaten and uneaten portions of the pizza. A circle, representing the pizza, is divided into six equal slices. Four of these slices are shaded, representing the eaten 4/6 portion. The remaining two slices are unshaded, highlighting the uneaten 2/6 portion. The shading clearly delineates the consumed and unconsumed portions of the pizza, making the concept of the fraction readily apparent.
<div style="display: flex; justify-content: center; align-items: center; width: 300px; height: 300px; border: 1px solid black;">
<svg width="300" height="300">
<circle cx="150" cy="150" r="120" style="stroke: black; fill: none;"/>
<path d="M 150 20 L 150 60 Z" style="stroke: black; fill: #ff0000;"/>
<path d="M 150 60 L 180 90 Z" style="stroke: black; fill: #ff0000;"/>
<path d="M 150 60 L 120 90 Z" style="stroke: black; fill: #ff0000;"/>
<path d="M 150 60 L 180 120 Z" style="stroke: black; fill: #ff0000;"/>
<path d="M 150 120 L 180 150 Z" style="stroke: black; fill: none;"/>
<path d="M 150 120 L 120 150 Z" style="stroke: black; fill: none;"/>
</svg>
</div>
Real-World Implications
Fractions aren’t just abstract math concepts; they’re fundamental to understanding and interacting with the world around us.
From meticulously measuring ingredients in the kitchen to calculating discounts at the store, fractions are woven into the fabric of daily life. Understanding fractions unlocks a deeper appreciation for how things work, especially in the realm of quantities and proportions.
Understanding fractions is crucial for practical applications. Whether it’s dividing a pizza fairly among friends, determining the amount of sugar needed for a recipe, or understanding the percentage of a sale, fractions provide a precise and efficient way to represent and manipulate quantities.
Marty devoured 4/6 of his pizza, leaving only a tiny fraction behind. Meanwhile, big news hit the retail world as JC Penney announced the sale of 120 stores, including two right here in Cincinnati jcpenney announces sale of 120 stores including two in cincinnati. Talk about a slice of retail history. I wonder if that impacted the pizza market in any way?
Maybe Marty’s pizza appetite was somehow related? It’s all a bit much, really.
Practical Applications in Daily Life
Fractions are essential for tasks ranging from cooking and baking to budgeting and calculating distances. A clear grasp of fractions allows for accurate measurements and calculations, crucial for avoiding mistakes in various scenarios.
- Cooking and Baking: Recipes often rely on fractions to specify ingredient amounts. For instance, a recipe might call for 1/2 cup of flour or 3/4 teaspoon of salt. Without understanding fractions, accurately following recipes becomes challenging, potentially impacting the final outcome.
- Portion Control: Fractions are fundamental to portion control. A nutritionist might recommend eating 1/4 of a cup of rice or 1/2 a banana. Fractions provide a precise way to divide portions into manageable and controlled sizes.
- Measurements: Fractions are ubiquitous in measurement. From measuring lengths with fractions of an inch or centimeters, to measuring liquids in fractions of a cup or liters, fractions are vital for accuracy in a wide array of tasks.
Fractions, Decimals, and Percentages: A Comparison
While fractions, decimals, and percentages are different ways of representing parts of a whole, they are closely related. Understanding the relationships between these concepts enhances your ability to solve problems efficiently.
| Concept | Representation | Example |
|---|---|---|
| Fractions | a/b (where a and b are integers, b ≠ 0) | 1/2, 3/4, 2/5 |
| Decimals | a numerical representation using a decimal point | 0.5, 0.75, 0.4 |
| Percentages | A fraction out of 100 | 50%, 75%, 40% |
Fractions, decimals, and percentages are interchangeable representations of parts of a whole. Converting between these representations is a crucial skill in various real-world applications.
Importance of Understanding Fractions in Everyday Situations, Including Food
A robust understanding of fractions is essential for making informed decisions in daily life, especially when dealing with food. This includes calculating portions, comparing prices, and planning meals.
- Food Shopping: Fractions can help you compare prices per unit. For instance, understanding that 1/2 a pound of ground beef costs $2.50, while a whole pound costs $5, can help you make cost-effective choices. This understanding directly influences financial decisions.
- Recipe Adaptation: Fractions are vital when adjusting recipes. If a recipe calls for 1/4 cup of milk and you need to double the recipe, you need to understand that you need 1/2 a cup of milk. Understanding fractions is directly linked to adjusting recipes for different serving sizes.
- Portion Control: The importance of portion control is directly related to understanding fractions, as accurate portions are based on fractions of the whole.
Final Conclusion: Marty Ate 4 6 Of His Pizza
In conclusion, Marty’s pizza-eating adventure offered a rich opportunity to explore the mathematical concept of fractions. We’ve seen how 4/6 of a pizza translates into various real-world scenarios, from the potential sizes of the pizza to the leftover portions. By understanding fractions, we can better comprehend portion control and the implications of these mathematical concepts in everyday life. The detailed analysis of pizza fractions will be invaluable to all pizza enthusiasts and math students.
Query Resolution
What if Marty’s pizza was a different shape, like a square or a rectangle?
The fraction 4/6 still represents the same portion of the whole pizza, regardless of the shape. The division into slices would adjust accordingly to accommodate the shape.
How many slices were on Marty’s pizza?
The provided information does not specify the number of slices. The calculation works regardless of the total number of slices.
What are some real-world applications of fractions, besides pizza?
Fractions are used in cooking, baking, measuring ingredients, and many other daily tasks. They are fundamental to understanding portions and ratios.
How do fractions relate to percentages?
Fractions and percentages are interchangeable ways of representing parts of a whole. 4/6 can be converted to a percentage.
